-
摘要:
应用霍普金森压杆(SHPB)实验装置, 通过改变透射杆为钢杆和铝杆, 对立方体聚甲基丙烯酸甲酯(PMMA)试样和两种梯台PMMA试样进行动态压缩实验. 利用高速摄影记录试样的压缩过程, 并结合力位移曲线分析试样的破碎过程, 探讨了冲击载荷作用下PMMA试样变形和广义扩散阻力的演化. 结果表明: 试样的破坏模式主要为接触端局部产生失效阵面, 然后失效阵面向试样内部扩展. 立方体试样在低速冲击下, 失效阵面优先在透射端产生; 在高速冲击下, 失效阵面在入射端先产生. 通过改变试样形状和透射杆材质后, 阵面的产生存在明显的弛豫现象, 并且失效阵面仅在入射端产生. 梯台试样破碎前的压缩变形是非均匀的, 试样内部应力状态和变形状态随着截面增加逐渐变小, 并且呈线性扩散分布. 通过应变分布结合剪切激活扩散方程, 得到失效阵面扩散过程中的广义扩散阻力分布情况; 失效阵面前后广义扩散阻力先增加后减小, 阻力的幅值与局部应变能的释放有关.
Abstract:Dynamic compression experiments on cubic polymethyl methacrylate (PMMA) specimens and two kinds of trapezoid PMMA specimens are carried by changing the transmission bars into steel bar and aluminum bar on the experimental device of split Hopkinson pressure bar (SHPB). The compression processes of PMMA specimens are recorded by high-speed photography, and the breakage processes of PMMA specimens are analyzed based on the force displacement curves and high-speed images. The evolutions of deformation and diffusion resistances of PMMA specimens under impact loading are discussed. The results show that the failure of the sample is caused mainly by the partial failure front at the contact end, and then the failure front propagates to the inside of the sample, s leading the sample to break. The failure front of cubic sample is generated preferentially at the transmission end under low speed impact and at the incident end under the higher speed impact. After changing the shape of the specimen and the material of the transmission bar, the relaxation phenomenon is prominent, and the failure front occurs only at the incident end. The compressive deformation of the trapezoid sample before breakage is non-uniform, and the stress and strain in the sample gradually decrease with the increase of the cross section, and show a linear diffusion distribution. The strain distribution and shear activation diffusion equation are used to obtain the generalized diffusion resistance distribution of the failure front. The generalized diffusion resistance increases first in front of the failure front and decreases after the failure front, and the amplitude of the generalized diffusion resistance is related to the release of local strain energy.
-
Key words:
- impact dynamics /
- stress-state adjustment /
- PMMA /
- stress diffusion
-
图 1 试样规格 (a) 立方体试样; (b) 梯台试样; (c) 梯台试样简图
Figure 1. Sample specifications: (a) Cube sample; (b) trapezoid sample; (c) diagram of the trapezoid sample.
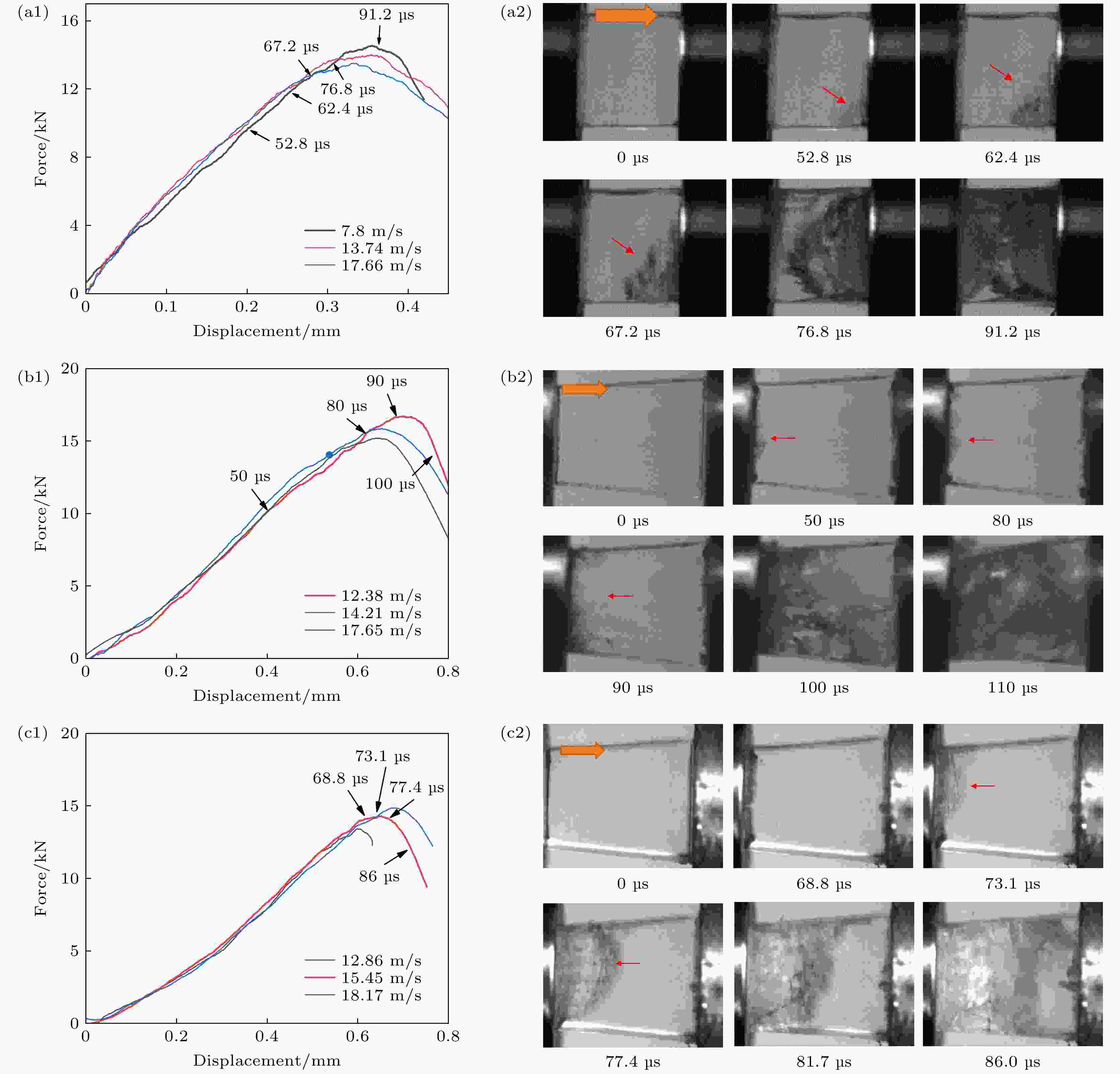
图 3 冲击过程中的载荷位移曲线和破碎过程 (a1) 透射杆为钢杆时立方体试样的力位移曲线; (a2) 冲击速度为7.8 m/s时立方体试样的破坏过程; (b1)透射杆为钢杆时梯台试样Ⅰ的力位移曲线; (b2) 梯台试样Ⅰ的破坏过程(冲击速度为12.38 m/s); (c1)透射杆为铝杆时梯台试样Ⅰ的力位移曲线; (c2) 透射杆为铝杆时梯台试样Ⅰ的破坏过程(冲击速度为15.45 m/s). 橙色箭头表示冲击方向
Figure 3. Load displacement curve and crushing process during impact: (a1) Load displacement curve of cube sample under steel transmission bar; (a2) cube sample deformation process under impact velocity 7.8 m/s; (b1) load displacement curve of trapezoid sample Ⅰ under steel transmission bar; (b2) trapezoid sample Ⅰ under steel transmission bar (impact velocity 12.38 m/s); (c1) load displacement curve of trapezoid sample Ⅰ under aluminum transmission bar; (c2) trapezoid sample Ⅰ under aluminum transmission bar (impact velocity 15.45 m/s). The orange arrow denotes the impact direction.
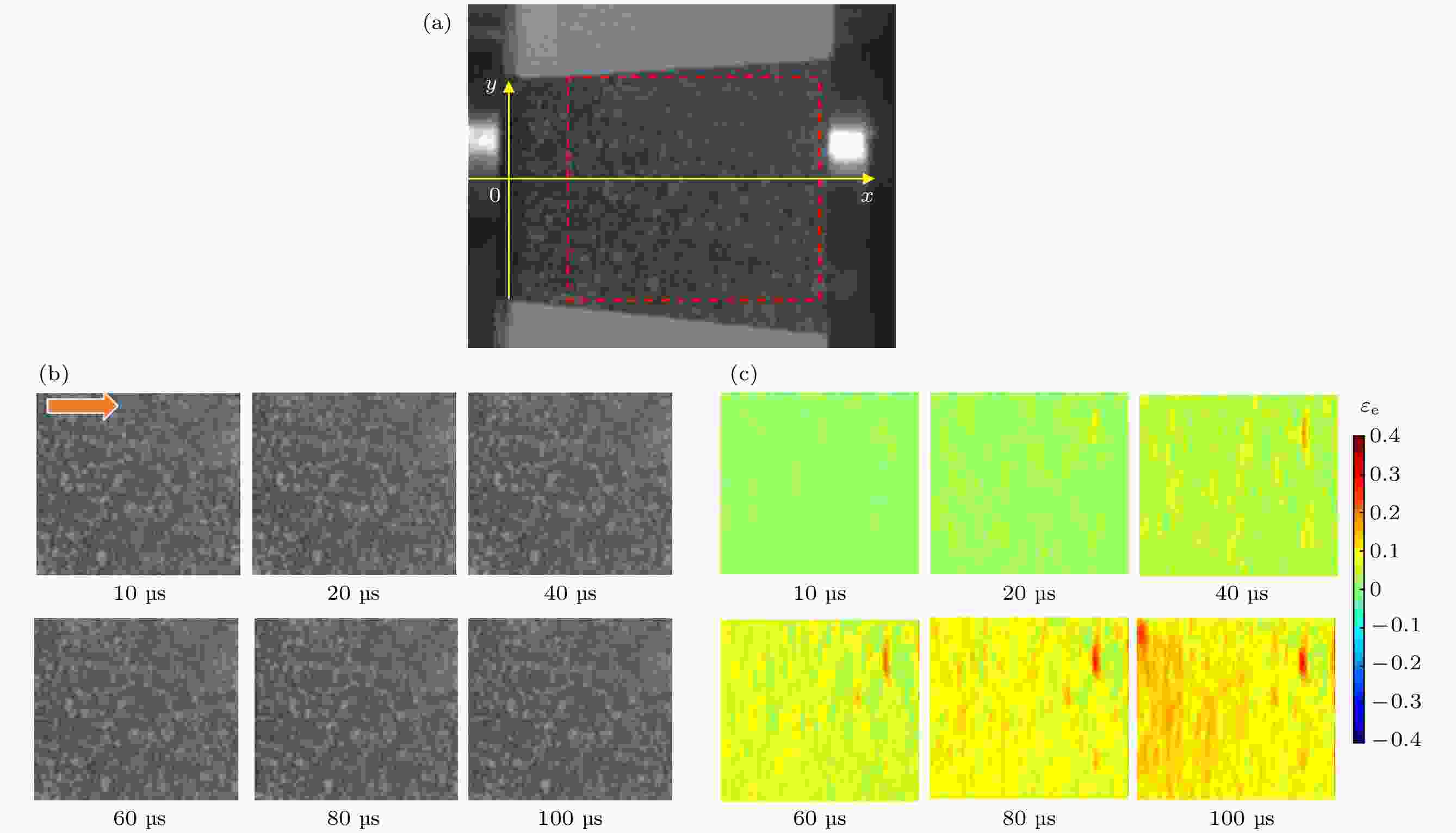
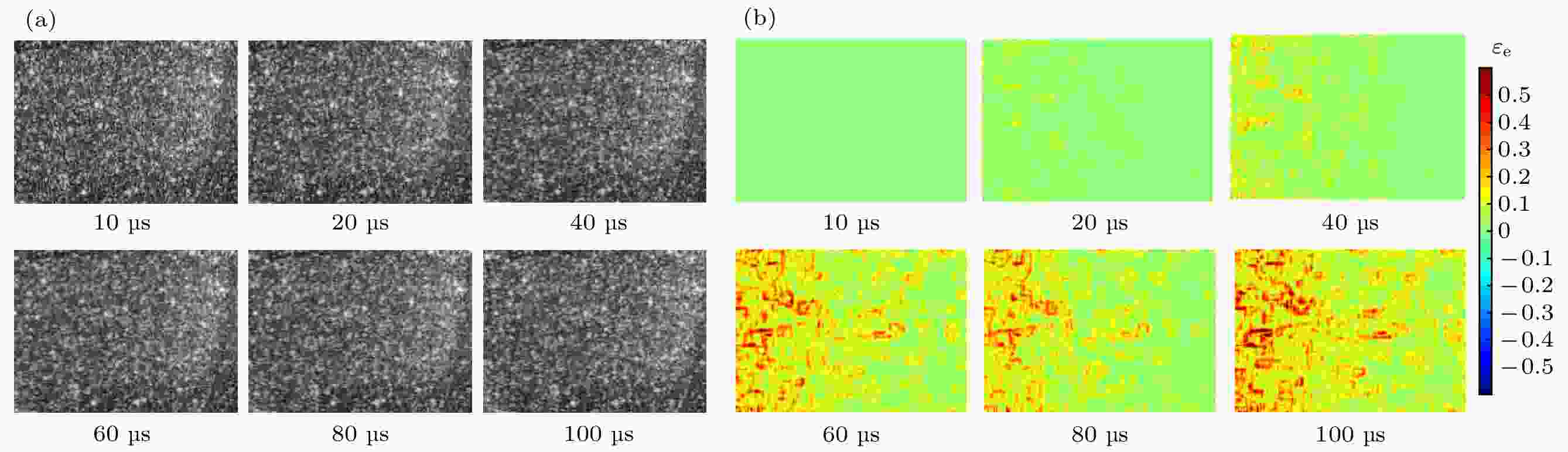
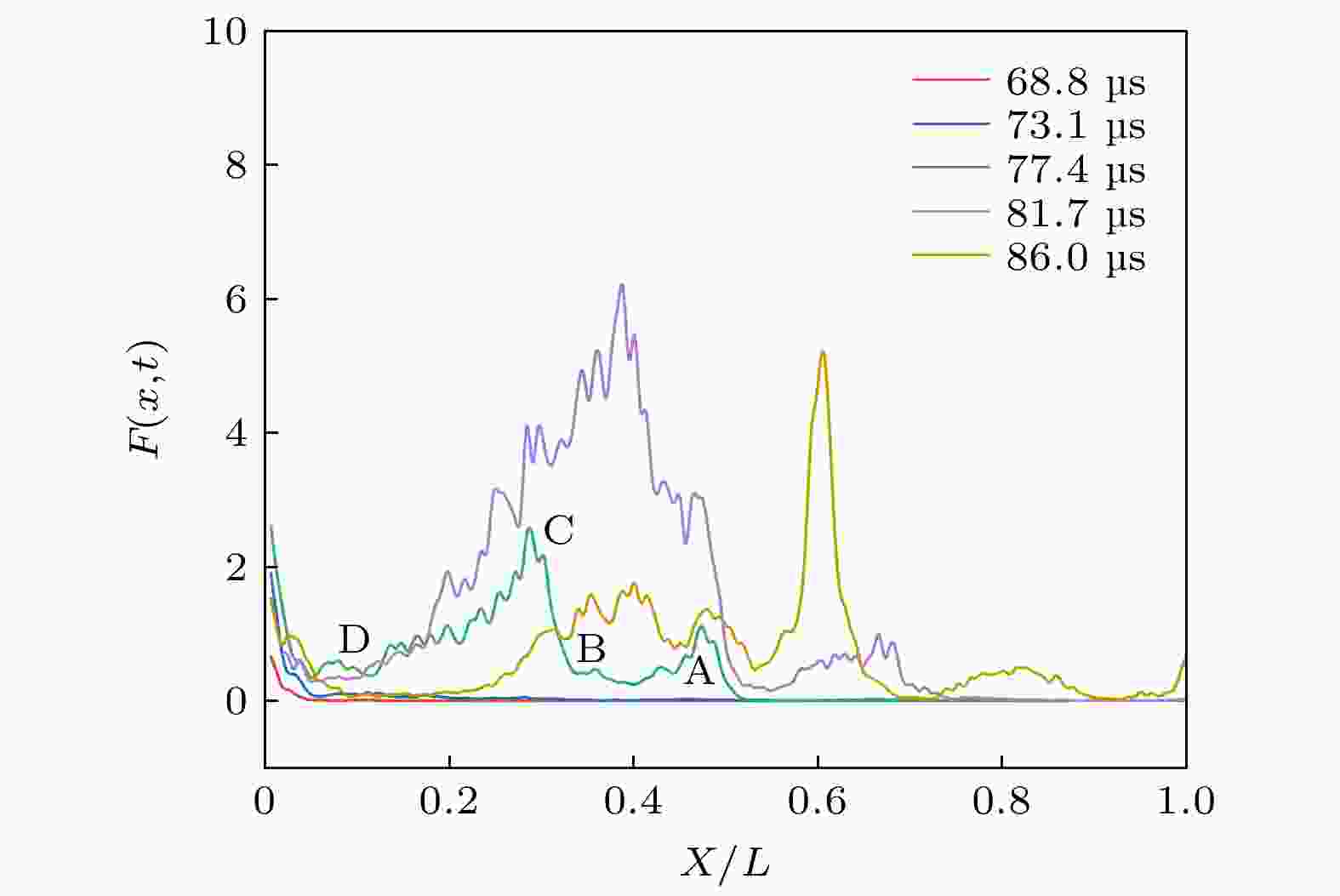
图 4 梯台试样Ⅰ在钢杆下的应变分布 (冲击速度13.3 m/s) (a) DIC计算区域; (b) 高速摄影图片; (c) 2 D等效剪应变场. (箭头表示冲击方向)
Figure 4. Strain distribution of trapezoid sample Ⅰ under steel transmission bar (impact velocity of 13.3 m/s): (a) Area of DIC calculation; (b) high speed images; (c) 2 D equivalent shear strain field (The arrow denotes the impact direction).
图 5 梯台Ⅰ试样在铝杆下的应变分布 (冲击速度16.21 m/s) (a) 高速摄影图片; (b) 2 D等效剪应变场(箭头表示冲击方向)
Figure 5. Strain distribution of trapezoid sample Ⅰ under aluminum transmission bar (impact velocity of 16.21 m/s): (a) High speed images; (b) 2 D equivalent shear strain field. (The arrow denotes the impact direction.)
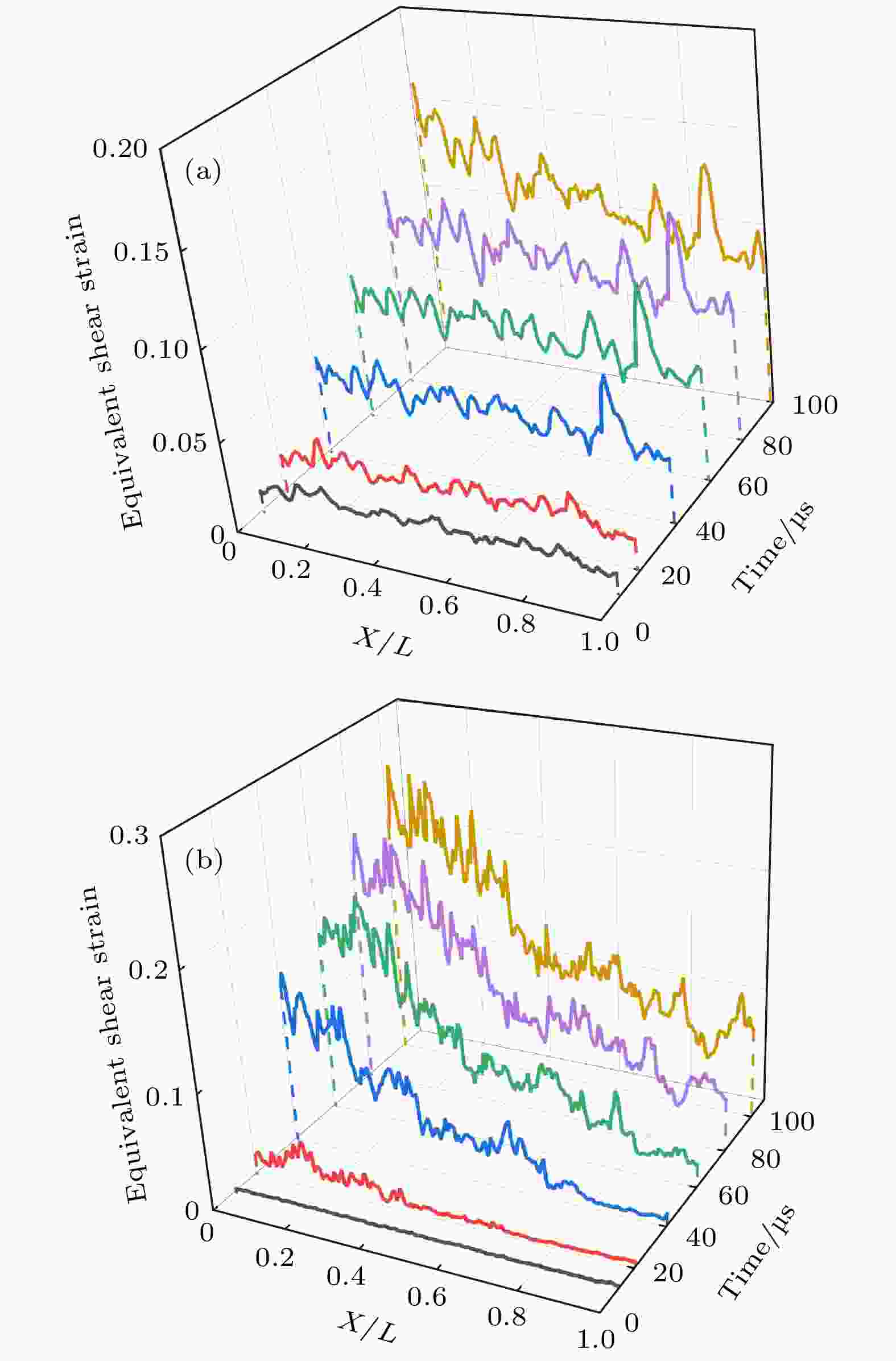
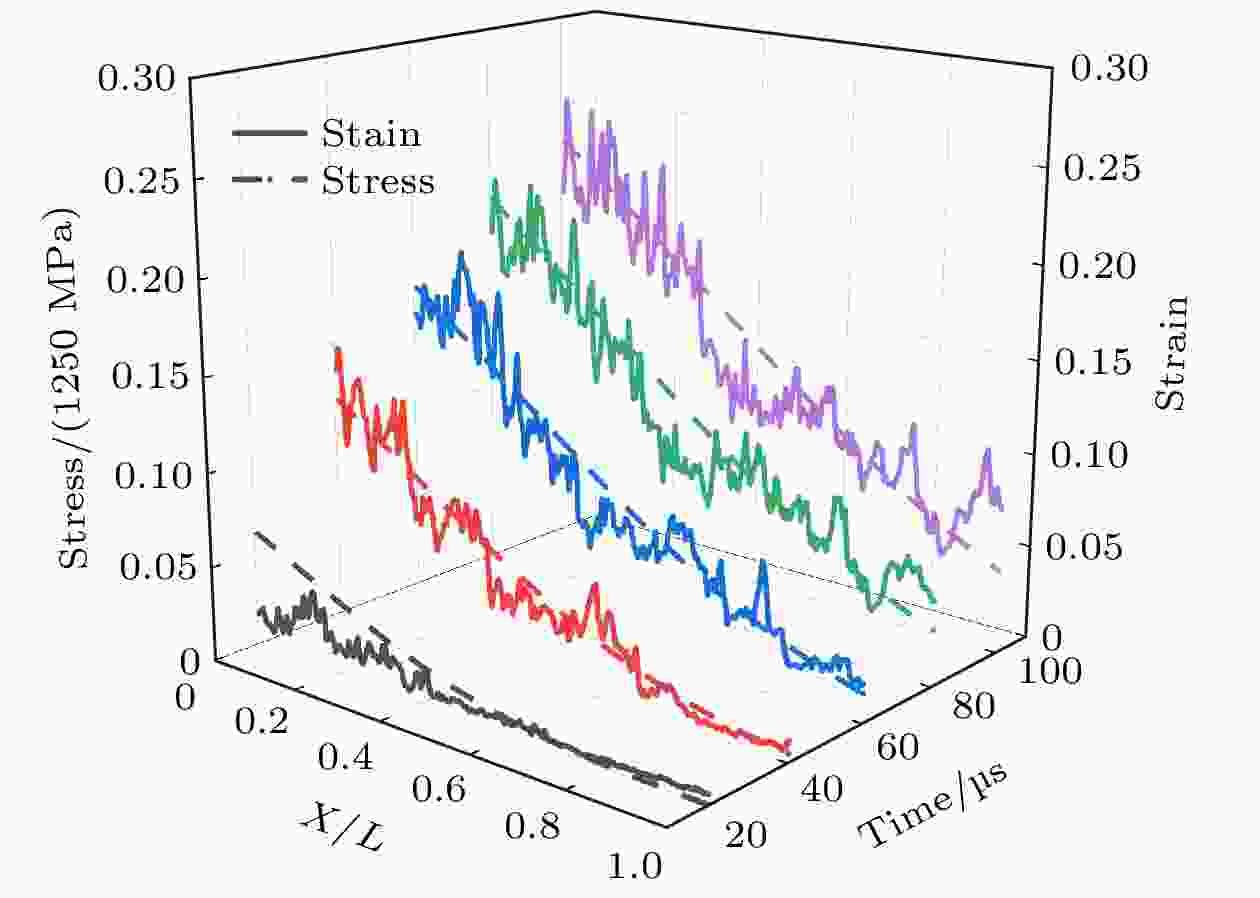
图 6 沿冲击方向的平均等效剪应变分布 (a) 梯台试样Ⅰ在冲击速度13.3 m/s透射杆为钢杆的应变分布; (b) 梯台试样Ⅰ在冲击速度16.21 m/s透射杆为铝杆的应变分布
Figure 6. Average equivalent shear strain distribution along impact direction: (a) Trapezoid sample Ⅰ under steel transmission bar (impact velocity of 13.3 m/s); (b) trapezoid sample Ⅰ under aluminum transmission bar (impact velocity of 16.21 m/s).
图 8 破碎时试样内的广义扩散阻力分布
Figure 8. Generalized diffusion resistance force distribution in the sample during breakage.
表 1 试样两端应力差统计
Table 1. Statistics of stress differences between two ends of sample.
试样 透射杆 应变率/s-1 应力差异 立方体 钢杆 600 <2.5% 梯台Ⅰ 500 20.4%—22.1% 梯台Ⅱ 600 33.8%—35.2% 梯台Ⅰ 铝杆 600 23.3%—25.5% 梯台Ⅱ 750 37.2%—43.1% 
下载: 导出CSV
-
[1] 徐松林, 单俊芳, 王鹏飞. 现代应用物理,2020,11:30101. doi: 10.12061/j.issn.2095-6223.2020.030101Xu S L, Shan J F, Wang P F. Mod. Appl. Phys., 2020, 11: 30101. (in Chinese) doi: 10.12061/j.issn.2095-6223.2020.030101 [2] 马棋棋, 熊迅, 郑宇轩, 周风华. 高压物理学报,2019,33:044101. doi: 10.11858/gywlxb.20190719Ma Q Q, Xiong X, Zheng Y X, Zhou F H. Chin. J. High Pressure Phys., 2019, 33: 044101. (in Chinese) doi: 10.11858/gywlxb.20190719 [3] Huang J, Xu S, Hu S. Rock Mech. Rock Eng., 2013, 47: 1727. [4] 陈兴, 马刚, 周伟, 赖国伟, 来志强. 物理学报,2018,67:146102. doi: 10.7498/aps.67.20180276Chen X, Ma G, Zhou W, Lai G W, Lai Z Q. Acta Phys. Sin., 2018, 67: 146102. (in Chinese) doi: 10.7498/aps.67.20180276 [5] Jiang H B, Xu S L, Shan J F, Wang D R, Liu Y G, Zhou L J, Wang P F. Powder Technol., 2019, 353: 359. doi: 10.1016/j.powtec.2019.05.028 [6] Shan J, Xu S, Liu Y G, Zhou L J, Wang P F. Powder Technol., 2018, 330: 317. doi: 10.1016/j.powtec.2018.02.009 [7] Potapov A V, Campbell C S. Powder Technol., 1997, 93: 13. doi: 10.1016/S0032-5910(97)03242-7 [8] Rasorenov S V, Kanel G I, Fortov V E, Abasehov M M. Int. J. High Pressure Res., 1991, 6: 225. doi: 10.1080/08957959108202508 [9] Espinosa H D. Mech. Mater., 1998, 29: 219. doi: 10.1016/S0167-6636(98)00016-7 [10] 冯晓伟, 李俊承, 王洪波, 常敬臻. 物理学报,2016,65:166201. doi: 10.7498/aps.65.166201Feng X W, Li J C, Wang H B, Chang J Z. Acta Phys. Sin., 2016, 65: 166201. (in Chinese) doi: 10.7498/aps.65.166201 [11] Anderson Jr C E, Bigger R P, Weiss C E. Int. J. Appl. Glass Sci., 2014, 5: 374. doi: 10.1111/ijag.12091 [12] Huang J Y, Li Y, Liu Q C, Zhou X M, Liu L W, Liu C L, Zhu H M, Luo S N. Phys. Rev. B, 2015, 92: 144101. doi: 10.1103/PhysRevB.92.144101 [13] Sheikh M Z, Atif M, Li Y L, Zhou F H, Raza M A, Dar U A, Gao G Z, Wang Y M. Constr. Build. Mater., 2021, 288: 123088. doi: 10.1016/j.conbuildmat.2021.123088 [14] 易洪昇, 徐松林, 单俊芳, 张鸣. 爆炸与冲击,2017,37:913. doi: 10.11883/1001-1455(2017)05-0913-10Yi H S, Xu S L, Shan J F, Zhang M. Explosion and Shock Waves, 2017, 37: 913. (in Chinese) doi: 10.11883/1001-1455(2017)05-0913-10 [15] 宋一平, 苗春贺, 单俊芳, 王鹏飞, 徐松林. 爆炸与冲击,2022,42:073103. doi: 10.11883/bzycj-2021-0244Song Y P, Miao C H, Shan J F, Wang P F, Xu S L. Explosion and Shock Waves, 2022, 42: 073103. (in Chinese) doi: 10.11883/bzycj-2021-0244 [16] 方继松, 王珠, 熊迅, 郑宇轩, 周凤华. 高压物理学报,2020,34:014101. doi: 10.11858/gywlxb.20190764Fang J S, Wang Z, Xiong X, Zheng Y X, Zhou F H. Chin. J. High Pressure Phys., 2020, 34: 014101. (in Chinese) doi: 10.11858/gywlxb.20190764 [17] Miao C H, Xu S L, Song Y P, Xie Y S, Yuan L Z, Wang P F. Powder Technol., 2022, 397: 117081. doi: 10.1016/j.powtec.2021.117081 [18] Liu D, Shen L, Guillard F, Einav I. Int. J. Impact Eng., 2016, 93: 222. doi: 10.1016/j.ijimpeng.2016.03.005 [19] 简世豪, 苗春贺, 张磊, 单俊芳, 王鹏飞, 徐松林. 高压物理学报,2021,35:024202. doi: 10.11858/gywlxb.20200629Jian S H, Miao C H, Zhang Lei, Shan J F, Wang P F, Xu S L. Chin. J. High Pressure Phys., 2021, 35: 024202. (in Chinese) doi: 10.11858/gywlxb.20200629 [20] Xing H Z, Zhang Q B, Braithwaite C H, Pan B, Zhao J. Rock Mech. Rock Eng., 2017, 50: 1611. doi: 10.1007/s00603-016-1164-0 [21] Zhou L, Xu S, Shan J, Liu Y, Wang P. Mech. Mater., 2018, 123: 1. doi: 10.1016/j.mechmat.2018.04.013 [22] Grady D. 2017 Phys. Shock Impact (Vol. 1) (London: IOP Publishing) pp2-57—2-68 [23] Mott N F. Proc. R. Soc. London,Ser. A, 1947, 189: 300. doi: 10.1098/rspa.1947.0042 [24] Feng R. J. Appl. Phys., 2000, 87: 1693. doi: 10.1063/1.372079 [25] 刘占芳, 常敬臻, 姚国文, 张凯, 李建鹏. 力学学报,2006,38:626. doi: 10.3321/j.issn:0459-1879.2006.05.008Liu Z F, Chang J Z, Yao G W, Zhang K, Li J P. Chin. J. Theor. Appl. Mech., 2006, 38: 626. (in Chinese) doi: 10.3321/j.issn:0459-1879.2006.05.008 -
下载:
点击查看大图
计量
- 文章访问数: 30
- HTML全文浏览量: 19
- PDF下载量: 0
- 被引次数: 0
京公网安备 11010502036328号 京ICP备17033152号